本节所介绍的FastBit是位图索引技术的集大成者，是一系列高级位图索引技术的集合，该项目最初设计目标是为美国国家高能物理实验提供支撑。
在FastBit中，两个核心创新点分别是：

字对齐混合压缩编码WAH，根据官方实验数据显示，其在高能物理实验中的索引性能是传统数据库的10倍以上，如图2.7所示；

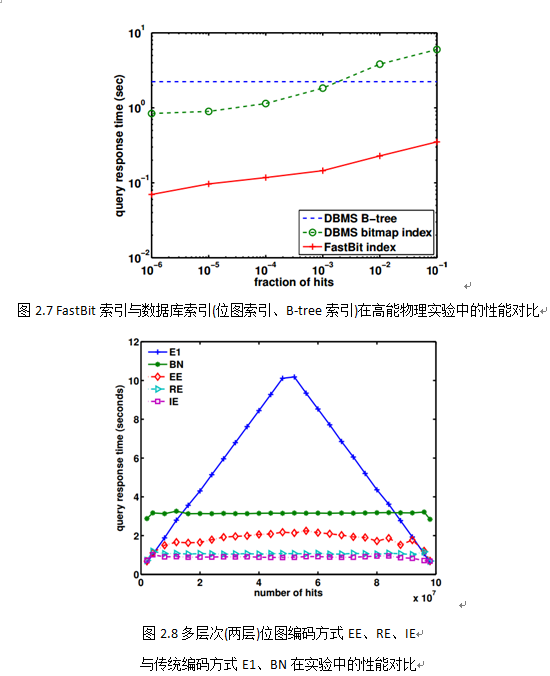
多层次(两层)位图编码方式，包括EE、RE和IE，与传统E1、BN编码的实验性能对比如图2.8所示。

目前，FastBit也成功应用于多种开源项目中，其中包括联机实时分析引擎Druid，其将FastBit中的高级索引技术与Hadoop的分布式文件系统HDFS结合起来。下面三节的主要工作就是介绍FastBit中核心创新点之一的WAH算法，和其改进算法Concise以及另辟蹊径的一种高级位图索引技术Roaring Bitmap。

1 WAH
WAH算法的核心在于两点：Word-Aligned和Hybrid。

Word-Aligned充分利用了现代CPU的特性，操作Word要比Byte效率高，所以WAH按照字对齐的方式对bitmap进行分组压缩；

Hybrid针对bitmap中既存在大量连续的“0”或“1”序列，又存在“0”“1”混合序列的情况，对这两种情况采用不同的压缩编码策略。

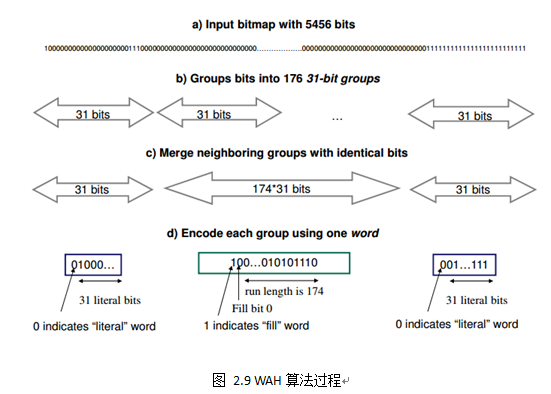
我们将Word分成两类：literal words和fill words，其中literal words用于“0”“1”混合序列，置最高位bit为0，剩余bits直接存储混合序列；fill words用于大量连续的“0”或“1”序列，置最高位bit为1，全“0”序列置次高位bit为0，全“1”序列置次高位bit为1，剩余bits存储该序列中“0”或“1”的个数，高位不足则用“0”补齐。图2.9给出了WAH算法的具体过程，下面我们结合图例进行介绍。

2 Concise Bitmap
Concise算法，全称叫做“Compressed‘n’ Composable Integer set”,是WAH算法的改进型。从上一节中我们可以看出，对于fill words，除去最高位和次高位，剩余的30bits最大可以表示2^30-1个连续的全“0”或全“1”序列，但是在实际使用场景中并不会出现，所以必然还有优化的空间。那么Concise算法就是高效压缩fill words中低n bits的改进型的WAH算法，或者说Concise算法解决如何压缩一个可组合的整数集合，或者可以是认为如何压缩一个稀疏的bitmap这一类问题。在实验中，Concise算法的压缩性能比WAH提高50%左右。

在Concise算法中，依然存在literal words和fill words的概念。其中，对于literal words，压缩策略与WAH基本一致，不过有一点差别，Concise置最高位为“1”来表示literal words，“0”表示fill words，如图2.10所示；对于fill words，除了最高位置“0”，次高位与WAH一致外，紧接着的5bits称为“Position bits”，代表了反转的位置(the position of a “flipped” bit)，表示在第一个31-bitsgroup中从第几位开始进行0、1反转。举例说明：

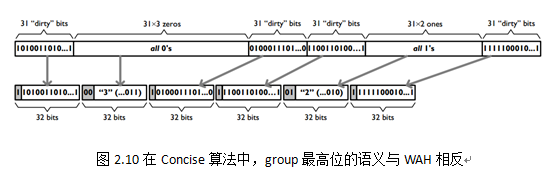
若Position bits = 0 (用二进制00000表示)，代表该word是一个纯粹的fill word，语义与WAH一致；

若Position bits = n (0, 32) (用五位二进制表示)，代表此fill word中第一个31-bitsgroup从第n位开始0、1反转；
而剩余的25bits表示除第一个31-bitsgroup外，该fill word还存放多少个连续的31-bits group，语义与fill words一致。我们可以看出，一个Word的最大的范围是31 + 2^25 * 31 = 1040187423 bit。

图2.11给出了一个由6个words组成的Concise算法样例，在Concise算法中，我们把bitmap看作是一个整数集合，也就是说如果此bitmap是一个literal word，那么位数则代表整数的个数，固定为31个；如果此bitmap是一个fill word，那么整数的个数为Count(31-bits group) * 31。下面我们就结合图例来理解Concise算法。

Word#0 是literal word，除去最高位，剩余31bit可以表示[0,30]这31个整数。

Word #1 是fill word，其中次高位为1，表示全“1”序列，Position bits为00000，表示此fill word语义与WAH一致，后25bits为1，表示包含2个31-bits group，第一个31-bits group表示[31,61]这31个整数，第二个31-bits group表示[62,92]这31个整数，即Word#1表示[31,92]这62个整数。

Word#2是fill word，次高位为0，表示全“0”序列，Position bits为00001，表示从第一个31-bits group的最低位开始0->1反转，后25bits为11101，表示除第一个31-bits group外，还有29个31-bits group，最大可以表示93(start) + 31 + 29 * 31 – 1 = 1022，即Word #2表示[93, 1022]这个区间内的整数。

Word #3 是literal word，包含31个整数，表示[1023, 1053]这个区间内的整数。

Word#4 是fill word，次高位为0，表示全“0”序列，Position bits为00000，表示该fill word的语义与WAH一致，后25bits为33554397(十进制表示)，表示共有33554398个31-bits group，最大可以表示1054 + 31 + 33554397 * 31 – 1 = 1040187391，即Word #4表示[1054, 1040187391]这个区间内的整数。

Word#5 是literal word，包含31个整数，表示[1 040 187 392, 1 040 187 422]这个区间内的整数。

3 Roaring Bitmap
上两节介绍的WAH和Concise压缩算法都是基于RLE原理，而Roaring bitmap则另辟蹊径，实验表明Roaring bitmap的压缩性能比RLE类更高。目前已知的使用Roaring bitmap的开源项目有Apache Spark、Apache Lucene和Druid.io。

Roaring Bitmap的主要思想是将32bit的整数分割成2^16个数据块，所有数据块共享相同的高16bit，低16bit则使用专门的容器来保存。容器可分为以下两种：

当一个数据块中的整数个数不超过4k时，我们认为是一个稀疏数据块，使用16bit/整数的有序数组容器(ArrayContainer)进行保存。

当一个数据块超过4096个整数时，我们认为是一个密集数据块，使用2^16bit的bitmap容器进行保存。

其中，阈值4k保证了每个整数不超过16bit，其中数组容器是固定bit(16 bit/整数)，而bitmap容器中每个整数不超过2^16 / 4k = 16 bit。那么，为什么选择4k这个阈值呢？因为根据上述公式，小于4k时，bitmap容器将会大于16bit/整数，大于4k时，数组容器大小会超过2^16 bit。总之，数据块基数较小时，使用数组更省空间，基数较大时，使用bitmap更省空间。

下面，我们简单介绍下基于Roaring bitmap的相关操作：

基数计算
每种容器（位图容器、数组容器）都使用一个计数器来记录它的基数，所以最多只需要累加2^16个计数器就可以完成。

数据查找
判断一个32bit的整数x是否存在，我们首先使用二分查找搜索x/2^16关联的容器。如果访问到的是数组容器，那么我们将继续迭代二分查找；如果访问到的是bitmap容器，那么我们就访问第x%2^16个bit，“0”表示不存在，“1”表示存在。

数据插入与删除
对于插入或者删除一个数据，我们首先需要找到对应的容器，当对象是一个数组容器时，我们使用二分查找在线性时间内插入或删除数据；当对象是一个bitmap容器时，我们设置对应bit的值并更新计数器。当删除一个整数时，bitmap容器的基数可能会减少到4k，退化为一个数组容器。当增加一个整数，一个整数容器的基数可能会超过4k，而变成一个bitmap容器。当上述两种情况发生时，Roaring bitmap会创建新的容器，更新计数器等并丢弃旧容器。
————————————————
版权声明：本文为CSDN博主「njpjsoftdev」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/njpjsoftdev/article/details/52955638

转载请注明：学时网 » 位图索引bitmap（三）：位图索引技术集合FastBit