计算化学中有时会要求我们计算两个向量的相似度，如做聚类分析时需要计算两个向量的距离，用分子指纹来判断两个化合物的相似程度，用夹角余弦判断两个描述符的相似程度等。计算向量间相似度的方法有很多种，本文将简单介绍一些常用的方法。这些方法相关的代码已经提交到github仓库

1. 基于距离的相似度计算方法

计算相似度时，一类常用的方法是计算两个向量之间的距离，两个向量间距离越近，则两个向量越相似。

1.1 欧式距离 (Euclidean Distance)

欧氏距离是一个通常采用的距离定义，指在n维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离就是两点之间的直线距离。n维向量间的欧式距离计算公式为：

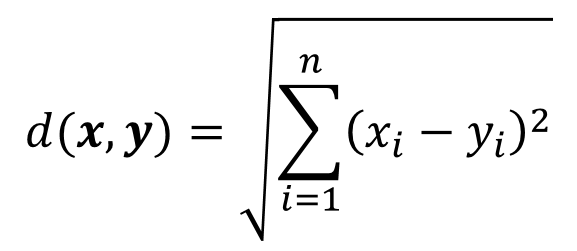
其中x向量为(x1,x2,…,xn)，y向量为(y1,y2,…,yn)。

1.2 曼哈顿距离 (Manhattan Distance)

曼哈顿距离是由十九世纪的赫尔曼·闵可夫斯基所创的词汇，是一种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和：

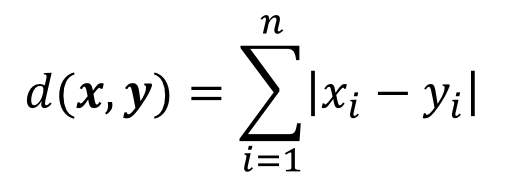
下图中，绿线表示两点间的欧氏距离，而红、蓝、黄线则为曼哈顿距离。

欧氏距离与曼哈顿距离（from Wikipedia）

1.3 切比雪夫距离 (Chebyshev Distance)

数学上，切比雪夫距离或是L∞度量是向量空间中的一种度量，二个点之间的距离定义为其各坐标数值差绝对值的最大值。以(x1,y1)和(x2,y2)二点为例，其切比雪夫距离为max(|x2−x1|,|y2−y1|)：

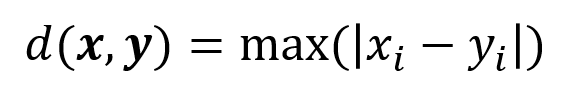
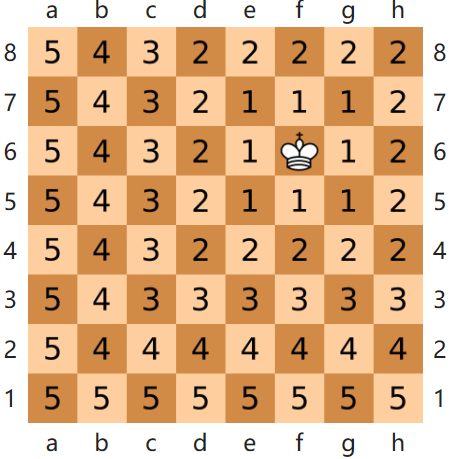
在国际象棋中，王的走法为可以横、竖、斜三个方向走动，但每次只能走一步。以下图为例，处于f6处的王到棋盘上各点所需要的最少步数即为该点到其他点的切比雪夫距离。因此切比雪夫距离又称棋盘距离。

1.4 闵可夫斯基距离 (Minkowski Distance)

闵氏距离不是一种距离，而是一组距离的定义。其计算公式为：

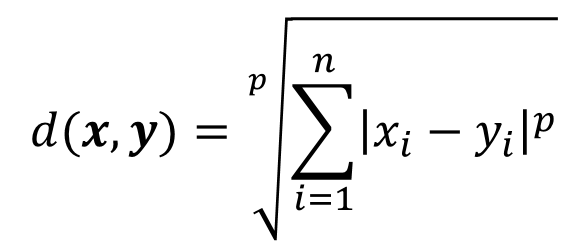
其中p为变参数。当p=1时，上式即为曼哈顿距离；当p=2时，上式即为欧氏距离；当p趋近无穷大时，易证上式即为切比雪夫距离。根据变参数的不同，闵可夫斯基距离可以表示一类距离。

闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。简单说来，闵氏距离的缺点主要有两个：（1）将各个分量的量纲 (scale)，也就是“单位”当作相同的看待了；（2）没有考虑各个分量的分布（期望、方差等）可能是不同的。

1.5 标准化欧氏距离 (Standardized Euclidean distance)

标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的计算方法是先将各个分量都先进行标准化，再求得标准化后的欧氏距离。

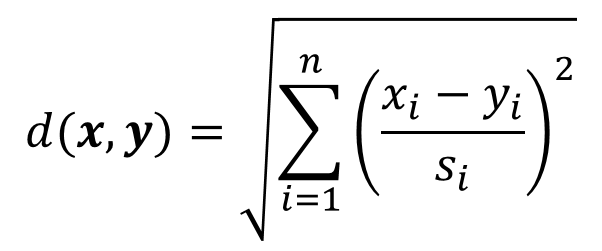
1.6 马氏距离 (Mahalanobis Distance)

有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到μ的马氏距离表示为：

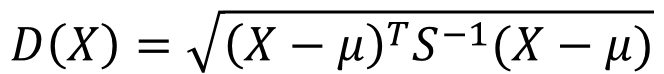
而其中向量Xi与Xj之间的马氏距离定义为：

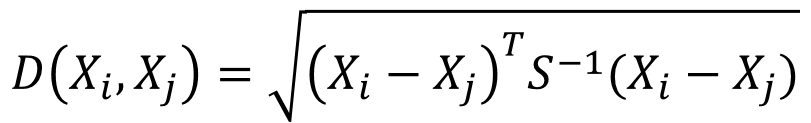
若协方差矩阵是单位矩阵（各个样本向量之间独立同分布），则马氏距离就是欧式距离；若协方差矩阵是对角矩阵，则马氏距离就是标准化欧式距离。

1.7 兰氏距离 (Lance Williams Distance)

兰氏距离的计算方法如下：

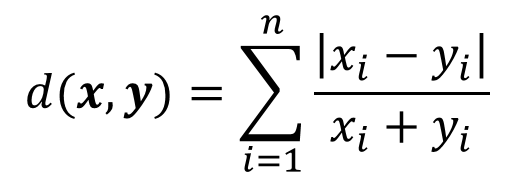
2. 夹角余弦

2.1 夹角余弦 (Cosine)

几何中夹角余弦可用来衡量两个向量方向的差异

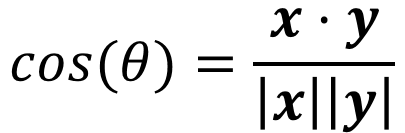
夹角余弦取值范围为[−1,1]。夹角余弦越大表示两个向量的夹角越小，夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向完全相反夹角余弦取最小值−1。

2.2 Tanimoto系数 (Tanimoto Coefficient)

Tanimoto系数是Cosine相似度的拓展。

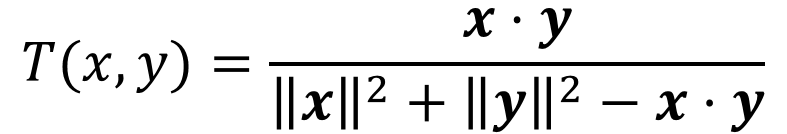
3. 相关系数

3.1 皮尔逊相关系数 (Pearson Correlation Coefficient)

皮尔逊相关系数一般用于计算两个定距向量间联系的紧密程度，它的取值在[−1,+1]之间。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性相关时，相关系数取值为1（正线性相关）或−1（负线性相关）

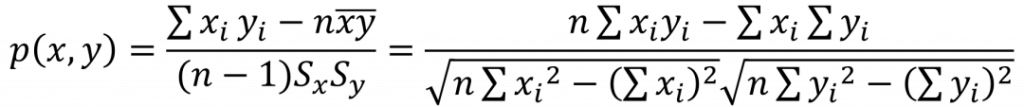
4. 集合观点下的相似度

4.1 杰卡德相似系数 (Jaccard similarity coefficient)

(1) 杰卡德相似系数

两个集合A和B的交集元素在A、B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示。

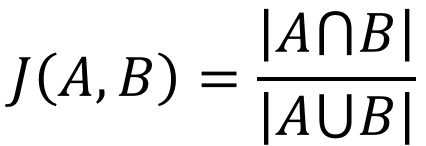
杰卡德相似系数是衡量两个集合的相似度一种指标。

(2) 杰卡德距离

与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示：

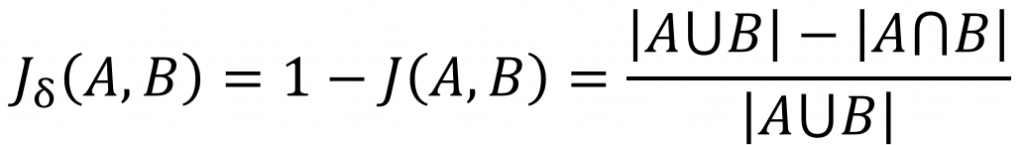
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

不足之处敬请批评指正！

参考资料：

转载请注明：学时网 » 计算向量间相似度的常用方法